| View previous topic :: View next topic |
| Author |
Message |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 01, 2003 11:25 am Post subject: need calculus help again Posted: Apr 01, 2003 11:25 am Post subject: need calculus help again |
 |
|
I posted a problem in Calculus I had a while back. Here is another. If someone could just get me pointed in the right direction it would help a lot. I think the concept of Optimization is supposed to be used here but I may be wrong here is the equation and problem:
f=(x^2)-(a^2)+300a+4ax-4480
I am trying to maximize f. I have to choose an "a" and after that another person chooses an "x". The other person is trying to minimize f. What "a" would I chose?
any help would be appreciated.
|
|
| Back to top |
|
 |
|
|
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 01, 2003 11:48 am Post subject: Posted: Apr 01, 2003 11:48 am Post subject: |
 |
|
Here's a hint:
If you take the derivative and set that equal to zero, a max or a min will occur there...
Let me know if you need more help...
Nick
________
Asatru (norse paganism) forums
Last edited by OttoNP on Mar 13, 2011 2:10 am; edited 1 time in total |
|
| Back to top |
|
 |
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 01, 2003 12:06 pm Post subject: Posted: Apr 01, 2003 12:06 pm Post subject: |
 |
|
Also, not sure exactly what you mean by maximize F, is there some kind of range given? F already goes to infinity as x goes to infinity and as x goes to negative infinity, you can't get bigger than that. Did you leave something out or word it different? I'm thinking you mean to maximize the min. of F.
Nick
________
Smoking Kills
Last edited by OttoNP on Mar 13, 2011 2:10 am; edited 1 time in total |
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 01, 2003 1:09 pm Post subject: Posted: Apr 01, 2003 1:09 pm Post subject: |
 |
|
| Yes, OttoNP, that is what I meant, maximize the min. of F. Sorry I wasn't more clear. Thanks for the help. also, how do you find the derivative of an equation with two variables in it? we haven't covered that yet. thanks.
|
|
| Back to top |
|
 |
Dragonlady8
Guest
|
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 01, 2003 4:12 pm Post subject: Posted: Apr 01, 2003 4:12 pm Post subject: |
 |
|
| I sure wish sites like that would actually help with these types of problems. I read through the pages, nothing helped. Thanks anyways.
|
|
| Back to top |
|
 |
kyle
Guest
|
 Posted: Apr 01, 2003 4:28 pm Post subject: Posted: Apr 01, 2003 4:28 pm Post subject: |
 |
|
| just do what Otto said, he is right
|
|
| Back to top |
|
 |
Jello John
Wakeboarder.Commie

Joined: 12 Jan 2003
Posts: 1936
|
 Posted: Apr 01, 2003 4:42 pm Post subject: Posted: Apr 01, 2003 4:42 pm Post subject: |
 |
|
| www.hotmath.com is a pretty valuable resource if you don't understand some math problems, you have the right textbook, and you if you use the website for help and not for just the answers.
|
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 01, 2003 5:06 pm Post subject: Posted: Apr 01, 2003 5:06 pm Post subject: |
 |
|
| I'm sure OttoNP is right, but how do you take the derivative of a function with two variables?
|
|
| Back to top |
|
 |
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 01, 2003 6:53 pm Post subject: Posted: Apr 01, 2003 6:53 pm Post subject: |
 |
|
Ok Jon, since a is a constant, you treat it as such. just pretend like it was a 2 or whatever. It is true that you get to pick a value for it, but once you pick it is a constant, different from x, and the derivative or any constant is still zero. I' ve got the answer and I'll tell you if you ask again, but try to figure it out with this hint:
So:
f=(x^2)-(a^2)+300a+4ax-4480
f'=2*x+4*a
_________________
http://www.corocks.com
I'd rather be wakeboarding...
Look Twice, Save a Life, Motorcycles are Everywhere
My lugnuts require more torque than your Honda can produce! |
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 01, 2003 8:16 pm Post subject: Posted: Apr 01, 2003 8:16 pm Post subject: |
 |
|
| alright, i got a=39.5. is this anywhere close to what you got? go ahead and explain the answer if you can. Once i see it, i can normally understand it. what i don't understand is that the other person could always pick some number to where f would equal a negative number.
|
|
| Back to top |
|
 |
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 02, 2003 4:04 am Post subject: Posted: Apr 02, 2003 4:04 am Post subject: |
 |
|
If you take the second derivitive, f''=2, since it is positive this means that when f'=0 it is indeed a min., which we already knew.
Solving f'=0, x=-2*a. This is where f will have a min, when x=-2*a. Now, you plug -2*a back into f to see what value f will have at its min.
f=(-2*a)^2-a^2+300*a+4*a(-2*a)-4480
f=4*a^2-a^2+300*a-8*a^2-4480
f=-5*a^2+300*a-4480
These are the possible values that f's min. will have based on the a you choose, you can see that the function is a parabola that goes to - infinitive as x goes to +/- infinitie, and has a max. So, you take the derivitive with respect to a and set it equal to zero.
f'=-10*a+300
Note that f''=-10, since it is negative you know it is indeed a max.
f'=0, -10*a+300=0, so a=30
From above the min occurs at x=-2*a, so x=-60.
Nick
________
Medical Marijuana States
Last edited by OttoNP on Mar 13, 2011 2:11 am; edited 1 time in total |
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 02, 2003 11:43 am Post subject: Posted: Apr 02, 2003 11:43 am Post subject: |
 |
|
| Thanks for all your help. I understand now. How would you do it if another person chose x first and then I choose a? I tried to do it the same way, except I treated x as a constant. I got an answer of a=-210, 3 different ways but that is not the right answer. Can you help me there?
|
|
| Back to top |
|
 |
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 02, 2003 12:04 pm Post subject: Posted: Apr 02, 2003 12:04 pm Post subject: |
 |
|
The min will always occur when x=-2*a, so you can make the min occur at whatever x you want; however, any a other than 30 will result in f's min not being the max it could be. F is a parabola, by changing the a value you are shifting it around. The min of F will lie somewhere on the function f=-5*a^2+300*a-4480. You can't really solve it assuming x is a constant since x isn't. You could make up a different problem where x is a constant and a is the variable, it is only common practice that makes x the variable, but once you decide what is constant and what isn't you can't change it.
When you get into some more advanced stuff you will treat variables as constants, like you'll get a function where f=x*y*z and then df/dx=y*z and df/dy=x*z and df/dx=y*z and df/dxyz=1, etc....
Nick
________
Honda Dylan 125 Specifications
Last edited by OttoNP on Mar 13, 2011 2:11 am; edited 1 time in total |
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 02, 2003 12:54 pm Post subject: Posted: Apr 02, 2003 12:54 pm Post subject: |
 |
|
I'm not quite catching what your saying. Maybe it would be best to totally start over with this part. This would be the question now:
f=(x^2)-(a^2)+300a+4ax-4480
I am trying to maximize f. A person chooses an "x", and after that, I have to choose an "a" . The other person is trying to minimize f. What "a" would I chose to maximize f?
|
|
| Back to top |
|
 |
Jon
Wakeboarder.Commie


Joined: 12 Jan 2003
Posts: 1176
|
 Posted: Apr 02, 2003 8:04 pm Post subject: Posted: Apr 02, 2003 8:04 pm Post subject: |
 |
|
| just bumping up
|
|
| Back to top |
|
 |
jbt200
Wakeboarder.Commie


Joined: 23 Feb 2003
Posts: 1041
City: Coldwater, MI
|
 Posted: Apr 02, 2003 8:12 pm Post subject: Posted: Apr 02, 2003 8:12 pm Post subject: |
 |
|
and i thought i was smart at math.. lol..guess not ahha
_________________
STFU and RIDE! |
|
| Back to top |
|
 |
OttoNP
Addict


Joined: 13 Jan 2003
Posts: 848
City: MI
|
 Posted: Apr 03, 2003 5:16 am Post subject: Posted: Apr 03, 2003 5:16 am Post subject: |
 |
|
The person will choose x=-2*a, that will always be where the min is. Then you would put x=-2*a back into the equation and follow the same steps to determine a.
If the person picked like 5 or something, the only way that would be the min of the function would be if you picked a as -2.5, but then the min of f wouldn't be the max it could be. Also, if you word it pick a to maximize f it doesn't make much sense since f will got to infinity regardless of the a you choose. You are trying to maximize the min of f.
________
YAMAHA LAGENDA SERIES HISTORY
Last edited by OttoNP on Mar 13, 2011 2:11 am; edited 1 time in total |
|
| Back to top |
|
 |
Slaytwebeling
Addict


Joined: 05 Feb 2003
Posts: 892
City: Houston
|
 Posted: Apr 03, 2003 6:10 pm Post subject: Posted: Apr 03, 2003 6:10 pm Post subject: |
 |
|
| Dang i am going to be in for it in 2 years lol
|
|
| Back to top |
|
 |
kyle
Guest
|
 Posted: Apr 03, 2003 6:40 pm Post subject: Posted: Apr 03, 2003 6:40 pm Post subject: |
 |
|
im not doing the whole problem because it would take to long because the numbers suck but im pretty sure im on the right track but i havent done this since the beginning of the year
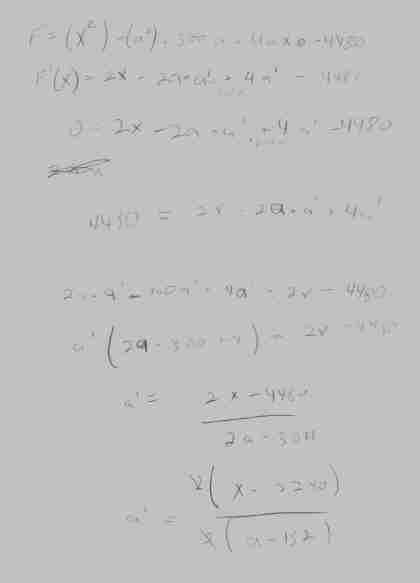
|
| Description: |
|
| Filesize: |
8.97 KB |
| Viewed: |
2453 Time(s) |
|
|
| Back to top |
|
 |
|
|
|